Evaluate search engine quality
ある日曜日にふと思いついたアイディアを実装して GitHub で公開してみました。それがこれ。
msmania/searchquality: Evaluate search engine quality
https://github.com/msmania/searchquality
検索エンジンの品質を数値化してみよう、という試みです。既に議論しつくされている話題であり、面接で聞かれる質問の定番でもありそうな問題です。私は検索エンジンの専門家ではないため基礎知識は全くなく、以下は単なる思いつきです。
さて、私は日常的に Bing と Google を検索エンジンとして使っていますが、どうにも Bing の検索結果は Google より劣っているように思えることが多々あります。最近明らかにおかしいと思った検索結果事例が↓の 2 つ。
- Bing で “seattle consulate japan” を検索したときに、領事館の公式サイト (http://www.seattle.us.emb-japan.go.jp/itprtop_ja/index.html) がトップに出てこないどころか、最初のページのどこにも出てこない。トップは yelp、2 番目は www.embassypages.com とかいう怪しいサイトになる。
- Bing で “gnu debugger” を検索したときに、GDB のプロジェクトのトップ https://www.gnu.org/software/gdb/ が最初のページに出てこない。
ちなみに Google 検索では、1. のケースは領事館のページがトップ、2. で GDB は最初のページの 2 番目に出てきます。
いずれの例にも共有していると考えられるのは、「ある検索キーワードに対して、大多数が正解と認めるような URL が定義できる」ことではないかと。基本的には、キーワードに対して、万人に共通する正解としての検索結果は定義できません。さらに同じユーザーであっても、検索するに至った目的やタイミングによって、その人が検索結果から最初にジャンプする URL 、もしくは最終的に満足を得た URL は変わるはずです。しかし上記の例については、その差異を加味したとしても最初のページに入っているべきなのではないかと思うのです。(ただし、広告からの収益と連動する今のビジネスモデルの場合、大人の事情によって公式サイトよりも優先しないといけないサイトがあって最初のページが埋まってしまうのかもしれませんが。)
結果の良し悪しを議論するのはさておいて、ある程度の確度で “正解っぽい URL” が定義できる検索キーワードのセットがあれば、それぞれの正解 URL が置かれた順位を集計して全体としての “品質” を数値化できるのではないか、というのが今回の思いつきです。そこで選んだのが Windows API の関数名と、その関数について記載している MSDN のページです。理由は以下の通り。
- 関数名のみをキーワードとして検索するとき、MSDN で使い方を調べたいパターンが多い。もし使用例を調べたいのなら “example”、トラブルシューティングならエラーコードなどの追加キーワードが入るはず。
- .NET のメソッドや POSIX 関数などの名前と重複するものが少ない。
- API はたくさんあるので、データ数を稼ぎやすい。
- Bing と MSDN はどちらも Microsoft のサービスであるが、MSDN に関しても経験上 Google の方がいい検索結果を出す気がする。Bing の場合、Windows CE の同名の関数のページに飛ぶことがある。
簡潔に言えば、この結果を受けて「Bing だめじゃん。ぷぷっ。」みたいなことをやりたいのです。
というわけで上記 GitHub のコードを使って、100 個の Windows API を選んで Google と Bing でそれぞれ検索してみました。本当は中国のBaidu (百度) でも試したかったのですが、中国語が読めなくて全然わからん・・。Yahoo は、どうせ中身が Google か Bing だったはずなのでパス。
で、結果なのですが、N=100 の検索結果に対して算術平均を取って Google が 0.119489、Bing が 0.1144965。あれ、ほとんど変わらない。この差がどのぐらいかというと、Google が最善解を 1 ページ目の 1 番目、次善解を 1 ページ目の 7.5 番目ぐらいに表示するのに対し、Bing は 1 番と 10 番あたりにに表示することを示しています。ちなみにこれは、検索結果ページがそれぞれ 10 の結果を表示する場合です。要は、検索結果ページの下の方の順位がちょこちょこっと変わっただけに過ぎないのです。なんか期待外れ・・・。もう少し別のデータセットで試してみたいところです。
いずれにしろ、定量的な議論はできるようになりました。以下、どうやってその数値を計算したかについて説明します。ただし、冒頭にも書いたように思い付きでやっているので、学術的に正しいかどうかは不明です。誰かこの記事をコピペして大学のレポートとして出して欲しい・・・。あと、詳しい人からのお便りは歓迎です。
まず、検索とは次のような操作であると定義します。
- インターネット上にある無数の URL を、検索キーワードによって「いい感じに」並び替える
- 検索結果は、有限個の URL を表示する「ページ」単位に分かれている
その結果を、ユーザーは以下のように判断します。
- ユーザーは、欲しい情報が載っている URL を開きたい
- ユーザーは、その URL を開くまでその URL に欲しい情報が載っているかどうか分からない
- ユーザーにとって、ページ間を移動する操作とページ内をスクロールする操作はともに面倒くさい
- ユーザーは、少ない操作で欲しい URL が開けるほど、その検索エンジンが高品質であると判断する
今回は、1 つの検索結果から品質を表すスコアとして 1 つのスカラー値を算出するものとします。
上述のように、今回は検索した関数名に対する MSDN の URL を正解と仮定するので、その正解の URL が上に来れば来るほど高得点になるような関数、例えば x 番目に来た時には逆数の 1/x をスコアとする、ことも可能です。しかし、1 番目に来たら 1 点で、2 番目に来たら 0.5 点、のように 2 倍も差が開いてしまうのは直感的に開きすぎているように思えます。
こういうときに機械学習などの分野でよく出てくるのが、確率密度関数です。というか t-SNE の論文やベイズ理論の本のせいで、確率密度がマイブームになっているので使ってみたかったのです。
Van der Maaten, L. J. P. & Hinton, G. E. Visualizing high-dimensional data using t-SNE. J. Mach. Learn. Res. 9, 2579–2605 (2008)
確率密度といえば、最初は何も考えずに標準正規分布から始めるのが(たぶん)流儀です。つまり、平均の付近で関数が極大になる性質を、検索結果の順位が上になるほど高いスコアを付加するという性質に適用します。そこで、まずページ内順位は無視して、とある検索結果が 1 ページ目に出たときのスコアを、確率変数が平均値の近傍にくる確率、2 ページ目に出たときのスコアをその外側の確率、というように適用することにします。すなわち数学的には、結果がページ i のどこかに存在するときのスコア p を
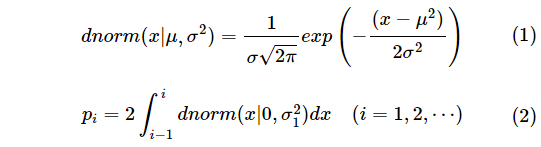
と定義します。確率密度関数を使う利点は、標準偏差 (もしくは分散) をパラメーターとして、スコアを簡単に調整できることです。いわゆる 68–95–99.7 rule というやつです。
68–95–99.7 rule - Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/68%E2%80%9395%E2%80%9399.7_rule
式 (2) に含まれる σ1 がパラメーターとなる標準偏差であり、σ1 = 1 と設定した場合、1 ページ目に検索結果が来るスコア p1 = 0.68、2 ページ目のスコア p2 = 0.95-0.68 = 0.27、となります。つまり σ1 は、そのユーザーがいかに最初のページを重要視するか (= ページ遷移を嫌がるか)、という目安になります。σ1 = 0.5 と設定すると、p1 = 0.95 になり、全体の検索結果のほとんどを占めます。
次にページ内順位を評価する方法ですが、これはベイズ理論でいうところの事後確率として考えるのが自然で、ページ i に検索結果が来た後に、もう一つ別の標準正規分布に従う確率を考慮します。ただし、ページ数とは異なって 1 ページにおける URL の数は有限です。そこで、正規分布グラフの山のうち、確率が低い麓の部分を切り捨てて、残った有限の面積を全体の確率の 1 として考えます。すなわち、ページ サイズが n で、ページ i の順位 j におけるページ内ランク q を
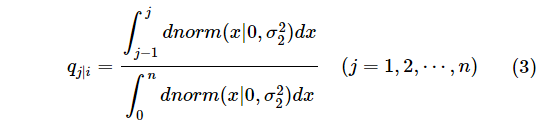
と定義します。式 (3) における偏差 σ2 は、そのユーザーがページ内の相対位置を重要視する程度 (= スクロールを嫌がるか) の目安になります。σ1 と同様、偏差はユーザーの性質の目安であるところがポイントです。別の方法として、ページ内ランクの偏差をページサイズ n と連動させる方法も考えられます。これは、同じユーザーがページ サイズの設定を変えて検索した時に、ページ内ランクに対する捉え方が変わるかどうか、という問題に帰結します。
長くなりましたが、上記のようにスコアの付け方を定義すると、総合的なランクは
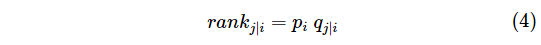
と定義できます。
例えば、2 ページはほとんど閲覧せず、ページ サイズは 10 でページ内は末尾までちゃんと見るユーザーとして (σ1, σ2, n) = (0.5, 10, 10) というパラメーターを使って、これを R でプロットすると以下のようになります。コードは GitHub の rank.R です。
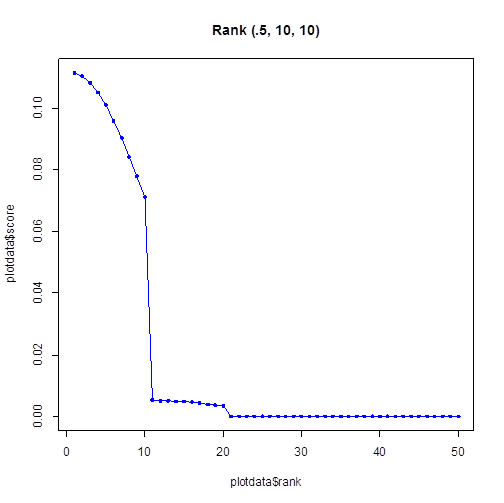
ちなみに Google も Bing も、既定のページ サイズは 10 です。仮にページ サイズを 100 にしたところでほとんどのユーザーは 10 位以降の検索結果はクリックされないのかもしれません。
ただし、例えばパソコンに詳しいパワー ユーザーの場合、もしくは仕事でどうしても必要な情報がある場合は、1 ページ目に結果が出ないからといって諦めずに次のページ、さらにその次のページをチェックする確率が高くなることが予想されます。そういったユーザーを想定する場合は、1 つ目の偏差を大きく設定します。
ページ遷移とスクロールのどちらを面倒くさがるか、という問題もあります。もしスクロールしながら結果をちまちま確認するのを嫌がって、さくさくページ遷移をしていくユーザーがいる場合、1 ページ目の最下位にある結果より、2 ページ目の先頭にある結果のほうが注目されやすいかもしれません。例えば、(σ1, σ2, n) = (1, 5, 20) のグラフは以下の通りです。
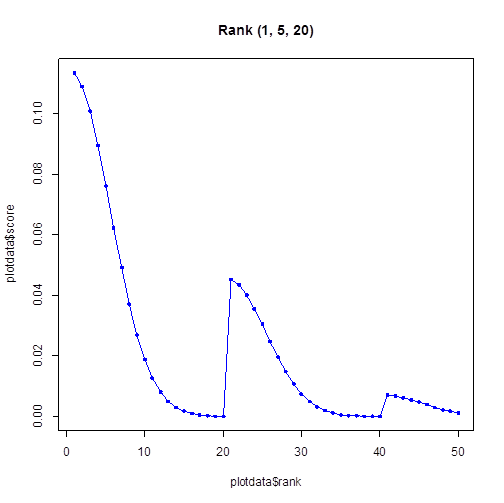
これで、検索結果内の位置をランクに変換する式ができました。グラフを見ても、わりとそれっぽい形をしています。この後残っているのは、実際の検索結果のタイトルと URL を見て、それが正解だったかどうかを判断することです。これは以下の Python の関数で判断しています。
def EvaluateSearchResultForMSDN(keyword, pair):
o = urlparse(pair[1])
titlelow = pair[0].lower()
return 1.0 if (o.hostname == 'msdn.microsoft.com') \
and (titlelow.startswith(keyword.lower())) \
and ('(windows)' in titlelow) \
else .0
URL のホスト名とタイトルをチェックしているだけの簡単なもので、正解なら 1、それ以外は全て 0 点にします。この点数と、位置毎のランクの積の合計を検索結果全体のスコアと定義しました。
もともとは、1 つのキーワードに対して正解は 1 つで、それを 1 点として計算する予定だったのですが、上記の関数だと、検索結果に正解が 2 つ含まれるキーワードがあることに気付きました。例えば “CreateWindow” を検索したときに CreateWindow だけでなく、CreateWindowEx の MSDN ページにも 1 点を与えるためです。この判断は迷いますが、経験上 CreateWindowEx も CreateWindow と同程度参考になると判断して、このまま同じ価値を持つ正解として扱うことにしました。
こうして算出したスコアの平均が、冒頭に書いた Google = 0.119489, Bing = 0.1144965 です。このときのパラメーターは (σ1, σ2, n) = (0.5, 10, 10) と設定したため、1 位のランクは 0.111370 になるのですが、平均がこれを超えているのは、正解が 2 つ以上あるキーワードが多かったからです。
以上が、冒頭のように Bing と Google を評価した理由です。より一般的には、MSDN だけでなく全ての検索結果にスコアを定義できるはずです。というか、検索エンジン自身がそう言ったスコア (Relevancy Ranking とか言うのがそれだと思う) を使っているはずです。コンピューター将棋やチェスでいうところの局面の評価値にも似ています。ある人が、人間の活動はほとんど評価値アルゴリズムに基づいている、みたいなことを言っていましたが、まさにそんな感じ。
ここから余談です。検索結果を REST API で得たあと、さてどうやってスコアを組み立てようか考えているときにふと思ったのが、映画 「ソーシャル ネットワーク」 の冒頭のこのシーン。
Eduardo Saverin: Hey, Mark.
Mark Zuckerberg: Wardo.
Eduardo Saverin: You guy’s split up?
Mark Zuckerberg: How did you know that?
Eduardo Saverin: It’s on your blog.
Mark Zuckerberg: Yeah.
Eduardo Saverin: Are you all right?
Mark Zuckerberg: I need you.
Eduardo Saverin: I’m here for you.
Mark Zuckerberg: No I need the algorithm you used to rank chess players.
Eduardo Saverin: Are you okay?
Mark Zuckerberg: We’re ranking girls.
Eduardo Saverin: You mean other students.
Mark Zuckerberg: Yeah.
Eduardo Saverin: You think this is such a good idea.
Mark Zuckerberg: I need the algorithm. I need the algorithm.
The Social Network Quotes - 'I invented Facebook.'
http://www.moviequotesandmore.com/social-network-quotes/
“I need the algorithm” と主張するザッカーバーグの気持ちが分かった。それが書きたかっただけです、はい。
もう一つまともな話を付け加えるとすれば、t-SNE の論文を最初に読んだときに、もともとの SNE の考え方で、高次元空間上における距離を条件付確率で表す発想の意味と、そのときの分散を恣意的に選べる理由が全く意味不明だったのですが、自分でやってみて何となくイメージが掴めるようになりました。t-SNE も自分で計算してみたいのですが、積分計算で躓いているダサい状況・・・。なんとかせねば。