MNIST with MDS in Python

前回の続きで、MNIST データを MDS で分析してみました。下記のブログの PCA の次のセクション “Optimization-Based Dimensionality Reduction” の最初のグラフ “Visualizing MNIST with MDS” の部分だけです。

Visualizing MNIST: An Exploration of Dimensionality Reduction - colah’s blog
http://colah.github.io/posts/2014-10-Visualizing-MNIST/

発想は PCA よりも単純で、今度は個々の MNIST データの 784 次元空間上の位置は考慮せず、2 つのデータのユークリッド距離をなるべく維持できるように全ての点を 2 次元平面上にプロットし直す、というものです。ただし、元の距離をなるべく維持する点の集合を PCA のようにまともに計算するのはおそらく不可能なので、任意の 2 点間を元の距離と同じ長さを自然長とするばねで繋いで、それを二次元空間のランダムな位置に投げ込み、物理法則に任せることで最適解を得る、というのがよくある方法のようです。以下の日本語の Wikipedia でも言及されているアプローチとほぼ同じです。

力学モデル (グラフ描画アルゴリズム) - Wikipedia
https://ja.wikipedia.org/wiki/%E5%8A%9B%E5%AD%A6%E3%83%A2%E3%83%87%E3%83%AB_(%E3%82%B0%E3%83%A9%E3%83%95%E6%8F%8F%E7%94%BB%E3%82%A2%E3%83%AB%E3%82%B4%E3%83%AA%E3%82%BA%E3%83%A0)

というわけで、今回はこれを Python で書いてみることにしました。Python 超初心者な上、エディタとして初めてまともに Emacs を導入してみたので、悪戦苦闘の毎日。しかもこれから書くように結果が微妙なことこの上ない。

R ではなく Python を選んだ理由は、matplotlib というモジュールを使ってインタラクティブなプロットを作るのが簡単そうだったからです。それと、R と SciPy はよく対比されているのでどちらも使ってみたかった、さらに言えば Python とは友達になっておいたほうが良さそうだった、などなど。

今回の環境はこんな感じ。

• Ubuntu 15.10 “wily”
• Python 2.7.10
• matplotlib (1.4.2)
• scipy (0.14.1)

というわけで書いたコードがこれ。

msmania/ems at purepython · GitHub
https://github.com/msmania/ems/tree/purepython

プロジェクト名の Euler Method というのは、微分方程式の近似解を得るための方法の一つです。実装は簡単だが精度が悪い、という理由から、基本的には使うべきではないらしい。他の方法としては、ルンゲ＝クッタ法とかがあります。

オイラー法 - Wikipedia
https://ja.wikipedia.org/wiki/%E3%82%AA%E3%82%A4%E3%83%A9%E3%83%BC%E6%B3%95

以下のページによると、「『この問題を解く場合、4次 のルンゲクッタだな』と一言いって、プログラムを書き始めると、出来るなと 思われること間違いなし」 らしいです。覚えておこう。

2 数値計算法
http://www.ipc.akita-nct.ac.jp/yamamoto/lecture/2003/5E/lecture_5E/diff_eq/node2.html

オイラー法とは、微小時間における速度、位置の変化を一次近似するだけです。上で紹介した Wikipedia の 「力学モデル」 で出てきた擬似コードがまさにそれです。

今回の Python コードで実装したのは、フックの法則から導き出される運動方程式と、ノードの位置を収束させるための摩擦力だけで、クーロンの法則によるノード間の反発力は完全に無視しました。また、フックの法則において弾性限度はないものとしています。動摩擦係数と静摩擦係数も区別していません。

ems.py の中の Field クラスに、ノード全ての速度と位置を行列として保持させて、オイラー法は行列計算として実装しています。5 フレームごとに計全体の運動エネルギーを計算して、特定の値を下回ったらシミュレーションを停止するようにもしています。

matplotlib の animation を使うと、H.264 形式の動画が簡単に作れるので、これでシミュレーション結果をアップロードしてみました。

MNIST with MDS in Python (N=200)
http://msmania.github.io/ems/purepython.htm

Windows だと、Internet Explorer と Firefox ではこの H.264 動画が再生できません。Chrome だと問題ないみたいです。Ubuntu 上の Firefox も問題なしでした。Windows Media Player 付属のデコーダーが対応していないらしく、Firefox は Windows のデコーダーに依存しているっぽいです。動画も暗号化アルゴリズムも独自実装している Chrome は便利。

.

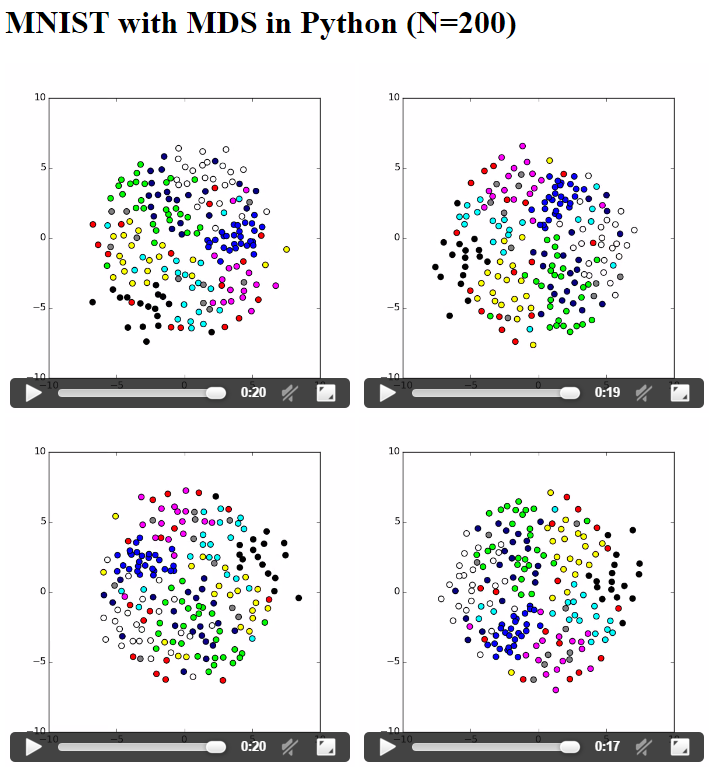MNIST のデータは N=10,000 もしくは 60,000 もあるのに、なんで N=200 なんだ、という話ですが、動作が遅すぎて計算できませんでした。上の N=200 の動画を作るだけでも、手元の環境でそれぞれ 6 分ぐらいかかります。ためしに N=1000 にしたところ、数時間経っても終わらなかったので断念。N=10,000 なんか 1 年経っても終わらないような。使っている CPU は Intel(R) Core(TM) i5-2520M CPU @ 2.50GHz で、アーキテクチャは Sandy Bridge です。

john@ubuntu1510:~/Documents/ems$ export N=200 
john@ubuntu1510:~/Documents/ems$ python mnist.py 200.mp4 
/usr/lib/python2.7/dist-packages/matplotlib/collections.py:571: FutureWarning: elementwise comparison failed; returning scalar instead, but in the future will perform elementwise comparison 
  if self._edgecolors == str('face'): 
time = 360.681 sec 
Done!

今回のモデルの場合、ばねのポテンシャル エネルギーが全て摩擦熱として失われるだけなので、系の運動エネルギーを毎回計算しなくてもシミュレーションの停止条件は求められそうです。しかし、試しにエネルギー計算をせずに 400 フレーム (= 20 秒) を生成させてみたところ、結局 7 分かかったので、エネルギー計算を省略しても問題は解決しません。

Python は書き方によって速度が大きく変わるらしいので、ひょっとするとコードを工夫すれば多少は改善するかもしれません。あとは Cython などの高速化ライブラリを使うとかだろうか。

Cython: C-Extensions for Python
http://cython.org/

しかし、ここまでやってようやく気づいてしまったのは、Field クラスは C++ で書いてしまったほうがよかったかもしれない、ということ。Sandy Bridge だから行列計算に AVX 命令を使えば高速化できそう。というか Python の SciPy は AVX 使ってくれないのかな。ノードにかかる運動ベクトルをラムダ式のリストにしてリスト内包表記で計算できるなんてエレガント・・という感じだったのに。

ビット演算ではないけど、↓ の話題に近くなってきている。コンピューター将棋でも、各局面を 81 次元の点として考えれば MNIST と大して変わらないのかもしれない。

プログラムを高速化する話 | やねうら王 公式サイト
http://yaneuraou.yaneu.com/2015/03/19/%E3%83%97%E3%83%AD%E3%82%B0%E3%83%A9%E3%83%A0%E3%82%92%E9%AB%98%E9%80%9F%E5%8C%96%E3%81%99%E3%82%8B%E8%A9%B1/

まだ知見を広められそうなので、もう少し MDS の演算で粘ってみようと思います。