Cooking MNIST with PCA in R

TensorFlow の初心者用チュートリアルを最初から読むと、MNIST (= Mixed National Institute of Standards and Technology) データベースと呼ばれる、手書きのアラビア数字を 28x28 のモノクロビットマップで表した画像データが出てきます。

MNIST For ML Beginners
https://www.tensorflow.org/tutorials/mnist/beginners/index.html

チュートリアルの冒頭で、この MNIST データをこねくり回してみたという記事へのリンクがあります。

Visualizing MNIST: An Exploration of Dimensionality Reduction - colah’s blog
http://colah.github.io/posts/2014-10-Visualizing-MNIST/

内容以前に、このウェブページ自体が MathJax という JavaScript ライブラリを使っていたり、ウェブでこんなことできるのか、という凄い代物で驚きます。著者の Christopher Olah という研究者の CV が公開されていて読めますが、まさに若き天才って感じ。流行の分野はやはり天才が多いんだろうなぁ。いいなぁ。

話が逸れました。さて、この記事の内容ですが、MNIST を視覚化する複数の数学的手法を紹介しています。より具体的には、28x28 のビットマップデータを、28x28 = 784 次元空間における 1 つの座標とみなして、いかにして人間が認識できる形にするか、すなわち 3 次元データにマップできるか、ということを試みています。

この発想自体が既に目から鱗だったわけですが、今回の記事では、具体的に出てくる次元下げの最初の手法についてトレースした結果を紹介します。残りの方法についても追って試す予定です。TensorFlow どこいったんだよ、という気もしますが、初めに基礎理論を固めておけば、あとの理解が楽になる気がするので端折らずにやります。

MNIST with PCA in R

そして最初の手法。PCA です。Principal component analysis の略。日本語だと主成分分析。どちらかというと Computer Science よりは、統計学で出てくる多変量解析の一手法です。PCA の次に MDS という手法も出てきますが、これも多変量解析の一つであり、統計学の理解が機械学習においては重要な気がします。

今回の内容を調べるにあたって、統計の初歩 (実は恥ずかしながら、これを調べる前は分散、偏差って何だっけレベルだった・・) から主成分分析の数学的背景までわりと真面目に復習したので、それについても今回の記事の最後に少し触れようと思います。

さて PCA ですが、統計と言えば R 言語だろう、という安易な考えで、Christopher Olah 氏がやったことを R で確かめてみます。デバッグをするわけではないのであまり重要ではないですが、環境は↓です。

Ubuntu 15.10 “wily”
R version 3.2.2 (2015-08-14) – “Fire Safety”

TensorFlow のチュートリアルに書いてありますが、MNIST データは以下のサイトからダウンロードできます。もしくは、TensorFlow に含まれている python スクリプトを使ってもいいです。

MNIST handwritten digit database, Yann LeCun, Corinna Cortes and Chris Burges
http://yann.lecun.com/exdb/mnist/

ファイルは 4 つあります。ファイル名に images とあるのがビットマップデータ。labels とあるのは、それぞれのビットマップがどのアラビア数字 (0-9) を書いたものなのかを表しています。要するにビットマップの答です。t10k のサンプル数が 10,000、train のサンプル数が 60,000 です。二つのサンプルに分かれている理由についてもチュートリアルのページに書かれていますが、学習用のデータと、学習後に使うデータを分けることで、学習が効果的かどうかを判断できる、ということです。

john@ubuntu1510:~/Documents/MNIST_data$ ls -l 
total 53672 
-rw-rw-r-- 1 john john  7840016 Nov 26 16:16 t10k-images-idx3-ubyte 
-rw-rw-r-- 1 john john    10008 Nov 26 16:16 t10k-labels-idx1-ubyte 
-rw-rw-r-- 1 john john 47040016 Nov 26 16:16 train-images-idx3-ubyte 
-rw-rw-r-- 1 john john    60008 Nov 26 16:16 train-labels-idx1-ubyte

ファイルのフォーマットについては、上記 Yann LeCun 氏のページの FILE FORMATS FOR THE MNIST DATABASE のセクションに書かれています。ヘッダーに次いで、配列を次元毎にべたーっと書き出しただけの形式です。

今回書いた R のコードは以下の通り。

readMNIST <- function(findex) { 
    imagefiles <- c("t10k-images-idx3-ubyte", "train-images-idx3-ubyte") 
    labelfiles <- c("t10k-labels-idx1-ubyte", "train-labels-idx1-ubyte") 
    fname <- paste0("~/Documents/MNIST_data/", imagefiles[findex]) 
    f <- file(fname, "rb") 
    seek(f, 4) # skip magic 
    n <- readBin(f, integer(), size=4, n=1, endian="big") 
    size.x <- readBin(f, integer(), size=4, n=1, endian="big") 
    size.y <- readBin(f, integer(), size=4, n=1, endian="big") 
    pixels <- readBin(f, integer(), size=1, n=n * size.x * size.y, signed=F) 
    close(f)

    images <- data.frame(matrix(pixels, ncol=28*28, byrow=T))

    fname <- paste0("~/Documents/MNIST_data/", labelfiles[findex]) 
    f <- file(fname, "rb") 
    seek(f, 4) # skip magic 
    n <- readBin(f, integer(), size=4, n=1, endian="big") 
    labels <- readBin(f, integer(), size=1, n, signed=F) 
    close(f)

    l <- list(labels, images) 
    names(l) <- c("labels", "images") 
    l 
}

drawMNIST <- function(mnist, idx) { 
    title <- mnist$labels[idx] 
    pixels <- as.integer(mnist$images[idx,]) 
    pixels <- matrix(pixels, 28, 28) 
    dev.new(width=5, height=5) 
    image(pixels[,28:1], col=grey(seq(0, 1, length = 256)), main=title) 
}

pcaMNIST <- function(images, scale) { 
    images.iszero <- apply(images, 2, function(col) { 
        return (var(col)==0 & var(col)==0) 
    }) 
    validData <- images[,names(subset(images.iszero, !images.iszero))] 
    prcomp(validData, scale=scale) 
}

drawRotation <- function(images, pca, range) { 
    images.iszero <- apply(images, 2, function(col) { 
        return (var(col)==0 & var(col)==0) 
    }) 
    zcols <- names(subset(images.iszero, images.iszero)) 
    l <- length(range) 
    zrows <- matrix(rep(0, length(zcols) * l), ncol=l) 
    rownames(zrows) <- zcols 
    pcs <- pca$rotation[,range] 
    pcs <- rbind(pcs, zrows) 
    rowindex <- as.integer(substring(rownames(pcs), 2)) 
    pcs <- pcs[order(rowindex),] 
    nul <- apply(pcs, 2, function(col) { 
        dev.new(width=5, height=5) 
        image(matrix(col, 28, 28)[,28:1], 
              col=c(hsv(2/3, seq(1, 0, length=10), 1), 
                    hsv(1,   seq(0, 1, length=10), 1))) 
    }) 
} 

以下 4 つの関数を定義しています。

readMNIST - MNIST ファイルを R のデータフレームとして読み込む関数
drawMNIST - 読み込んだビットマップのデータフレームをグラフィカル表示する関数
pcaMNIST - PCA を実行する関数
drawRotation - PCA 結果から、主成分をグラフィカル表示する関数

まずはファイルを読み込んでビットマップを表示してみます。

> source("MNISTCook.R") 
> mnist10k <- readMNIST(1) 
> mnist60k <- readMNIST(2) 
> drawMNIST(mnist60k, 1) 
> drawMNIST(mnist60k, 2) 
> drawMNIST(mnist60k, 3) 
> drawMNIST(mnist60k, 4)

上記のコードで、t10k, train の両方のデータを読み込んだ後、train データに含まれる 60,000 枚のビットマップのうちの最初の 4 枚を表示します。こんな感じ↓。チュートリアルの最初のページにある画像と一致していますね。

ちなみに、Raw データは、od コマンドで簡単に確かめることも出来ます。例えばこれが一枚目。

john@ubuntu1510:~/Documents$ od -tx1 -v -w28 -j16 -N784 MNIST_data/train-images-idx3-ubyte 
0000020 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
0000054 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
0000110 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
0000144 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
0000200 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
0000234 00 00 00 00 00 00 00 00 00 00 00 00 03 12 12 12 7e 88 af 1a a6 ff f7 7f 00 00 00 00 
0000270 00 00 00 00 00 00 00 00 1e 24 5e 9a aa fd fd fd fd fd e1 ac fd f2 c3 40 00 00 00 00 
0000324 00 00 00 00 00 00 00 31 ee fd fd fd fd fd fd fd fd fb 5d 52 52 38 27 00 00 00 00 00 
0000360 00 00 00 00 00 00 00 12 db fd fd fd fd fd c6 b6 f7 f1 00 00 00 00 00 00 00 00 00 00 
0000414 00 00 00 00 00 00 00 00 50 9c 6b fd fd cd 0b 00 2b 9a 00 00 00 00 00 00 00 00 00 00 
0000450 00 00 00 00 00 00 00 00 00 0e 01 9a fd 5a 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
0000504 00 00 00 00 00 00 00 00 00 00 00 8b fd be 02 00 00 00 00 00 00 00 00 00 00 00 00 00 
0000540 00 00 00 00 00 00 00 00 00 00 00 0b be fd 46 00 00 00 00 00 00 00 00 00 00 00 00 00 
0000574 00 00 00 00 00 00 00 00 00 00 00 00 23 f1 e1 a0 6c 01 00 00 00 00 00 00 00 00 00 00 
0000630 00 00 00 00 00 00 00 00 00 00 00 00 00 51 f0 fd fd 77 19 00 00 00 00 00 00 00 00 00 
0000664 00 00 00 00 00 00 00 00 00 00 00 00 00 00 2d ba fd fd 96 1b 00 00 00 00 00 00 00 00 
0000720 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 10 5d fc fd bb 00 00 00 00 00 00 00 00 
0000754 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 f9 fd f9 40 00 00 00 00 00 00 00 
0001010 00 00 00 00 00 00 00 00 00 00 00 00 00 00 2e 82 b7 fd fd cf 02 00 00 00 00 00 00 00 
0001044 00 00 00 00 00 00 00 00 00 00 00 00 27 94 e5 fd fd fd fa b6 00 00 00 00 00 00 00 00 
0001100 00 00 00 00 00 00 00 00 00 00 18 72 dd fd fd fd fd c9 4e 00 00 00 00 00 00 00 00 00 
0001134 00 00 00 00 00 00 00 00 17 42 d5 fd fd fd fd c6 51 02 00 00 00 00 00 00 00 00 00 00 
0001170 00 00 00 00 00 00 12 ab db fd fd fd fd c3 50 09 00 00 00 00 00 00 00 00 00 00 00 00 
0001224 00 00 00 00 37 ac e2 fd fd fd fd f4 85 0b 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
0001260 00 00 00 00 88 fd fd fd d4 87 84 10 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
0001314 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
0001350 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
0001404 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
0001440 

次に、PCA を実行します。R で PCA を行う関数は複数ありますが、ここでは prcomp 関数を使っています。ググって見つけたサイトが prcomp を使っていたからです。理由なんてそんなもんです。t10k と train のそれぞれのデータを PCA にかけます。train の方は 1 分ぐらいかかりました。

> pca10k <- pcaMNIST(mnist10k$images, F) 
> pca60k <- pcaMNIST(mnist60k$images, F)

PCA を実行した後、算出された成分のうち第一主成分から第四主成分を 28x28 のビットマップにプロットしたものを見てみます。というのも、Christopher Olah 氏が第二主成分までのプロットを記事に載せているからです。

> drawRotation(mnist60k$images, pca60k, 1:4) 
> drawRotation(mnist10k$images, pca10k, 1:4) 

上記一行目のコードで、train データについてのプロットが表示されます。上 2 つの主成分は、Christopher Olah 氏の載せている結果と同じと考えてよさそうです。

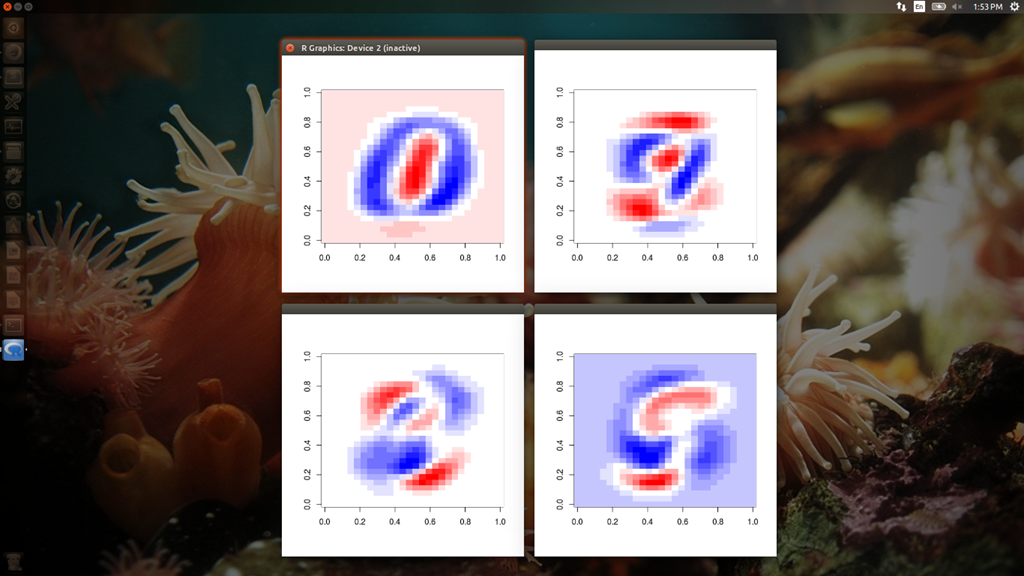
次に t10k の方から導出した主成分です。なぜかベクトルの向きが反転 (青と赤が逆) したようですが、向きを逆にすれば trainデータから導出された主成分とほぼ同じと見て問題なさそうです。

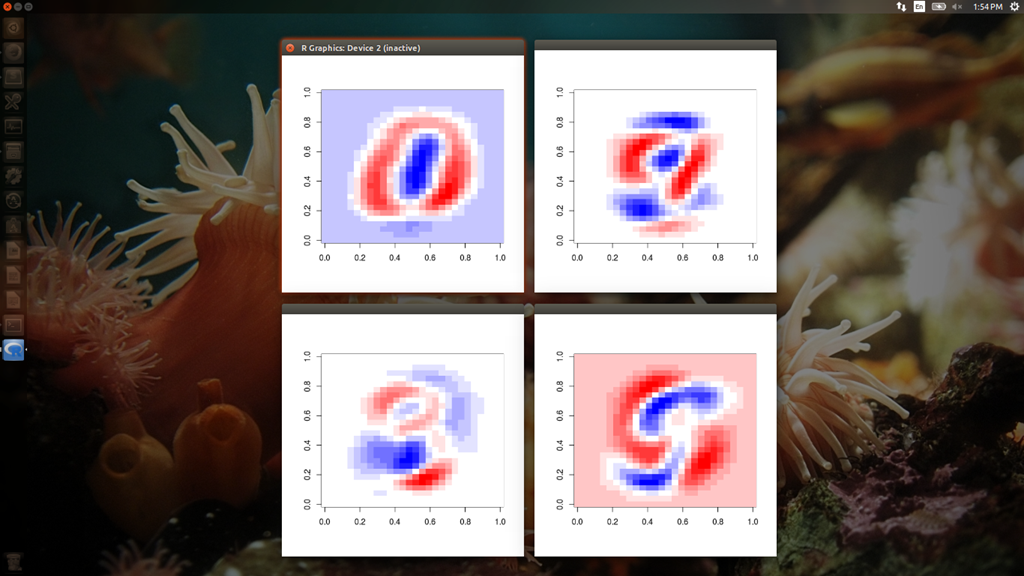
この後、Christopher Olah 氏の記事では、MNIST データを第一主成分と第二主成分の 2 次元座標にプロットした結果を示した上で、あまり nicely じゃないと結論付けて MDS を使った分析に移ります。ちょっと気になったのは、彼が累積寄与率に関する議論をしていないことです。まあ彼からすれば PCA なんて当て馬で大して議論する気もなかったのでしょうが、せっかく R のデータが手元にあるので、寄与率を見てみます。

> summary(pca10k)$importance[,1:4] 
                             PC1       PC2       PC3       PC4 
Standard deviation     587.63781 509.20428 459.38799 431.82659 
Proportion of Variance   0.10048   0.07544   0.06141   0.05426 
Cumulative Proportion    0.10048   0.17592   0.23733   0.29158

> summary(pca60k)$importance[,1:4] 
                             PC1       PC2       PC3       PC4 
Standard deviation     576.82291 493.23822 459.89930 429.85624 
Proportion of Variance   0.09705   0.07096   0.06169   0.05389 
Cumulative Proportion    0.09705   0.16801   0.22970   0.28359 

第二主成分までを採用したとして、寄与率は 17-18% であり、仮に第四主成分まで使っても 70% 以上の情報が失われることが分かります。巷の情報では、寄与率が 70 もしくは 80% を超えるように主成分を使うみたいなので、確かに 2 次元プロットが微妙なのも頷けます。と言っても、元データが 784 次元もあり、変換前の次元 2 つでは 2/784 = 0.255% しか寄与率がないことを考えると PCA はやっぱり強力、ということにはなります。

ここからは余談ですが、最初 pcaMNIST 関数を書いたとき、何をとち狂ったか、MNIST データを標準化した上で PCA にかけていました。すると以下のような全然違う主成分が得られます。この主成分がどんな意味を持つのかについては特に何も考察していませんが、元データがビットマップであり、各次元の単位は共通であることを考慮すると、標準化ダメ絶対、でしょうかね。

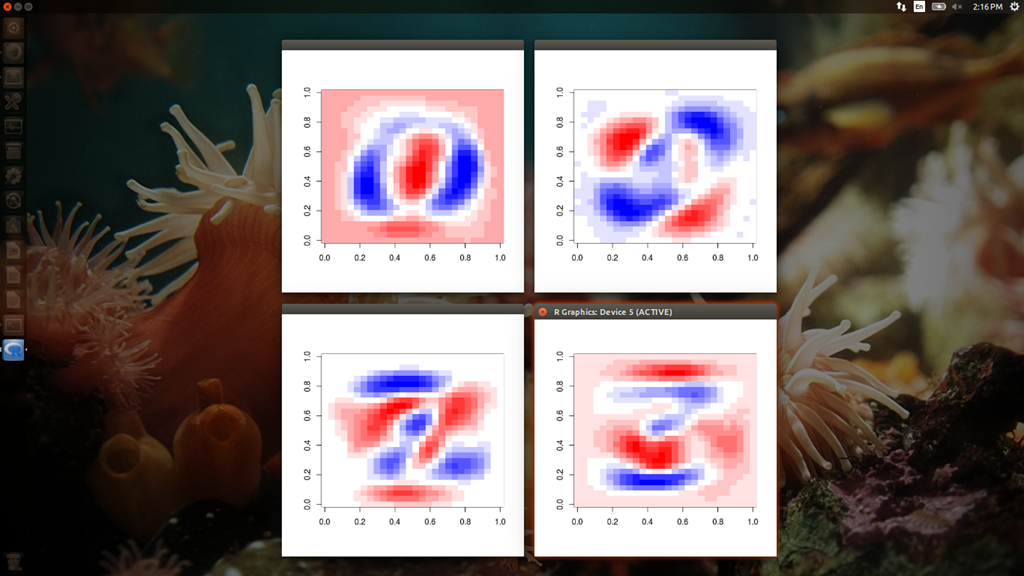
おまけ - PCA とは何か。どうやって計算するのか。

ここからは TensorFlow はもとより、MNIST とも関係なくなります。

PCA、すなわち主成分分析は、ちょっとググって見たところ一般に広く知られている手法で、需要予測などのマーケティングや、野球選手の戦力分析など、幅広い分野で使われているようです。一般的には次元下げが目的ですが、数学的には単なる座標変換であり、変換後の軸に対する振れ幅、すなわち分散が最大になるように決めた変換です。イメージとしては、以下のサイトの冒頭の図が分かりやすいです。

高校数学の基本問題 - Excelを用いた主成分分析
http://www.geisya.or.jp/~mwm48961/statistics/syuseibun1.htm

一次変換によって N 次元のデータを別の N 次元に変換するわけですが、各次元がデータに寄与する割合を変えて、なるべく少ない次元で多くの情報量を保持するように変換を決めて、その次元を主成分、と呼んでいるわけです。

面白いことに、主成分は、元データの分散共分散行列の固有ベクトルとして求まります。これを数学的に検証している日本語のサイトはさすがに少なかったのですが、以下の 2 つのサイトがとても参考になりました。

統計学復習メモ10: なぜ共分散行列の固有ベクトルが単位主成分なのか (Weblog on mebius.tokaichiba.jp)
http://ynomura.dip.jp/archives/2009/03/10.html

統計学入門－第16章
http://www.snap-tck.com/room04/c01/stat/stat16/stat1601.html

実際にこの計算を自分でも書き下してみたところ、PCA というのは数学的に美しいのが実感できました。ただし、計算の一番のポイントであるラグランジュの未定乗数法の証明はスキップしました。だって以下のサイトに、証明は単純ではないと書いてあるし。

ＥＭＡＮの物理学・解析力学・ラグランジュの未定乗数法
http://homepage2.nifty.com/eman/analytic/lag_method.html

ラグランジュの未定乗数法を除いても、大学で線形代数は苦手だったのでかなり理解するのに苦労しました。あと行列の偏微分はたぶん初見。それ以前に手で数式を解く感覚が完全に失われていたので取り戻すのに時間がかかりましたが。たまには数学をやって頭を柔らかくしないと駄目だなぁ・・あれ、また話が逸れている。

数学的な証明をこのブログに載せるのは面倒なのでパスするとして、では本当に分散共分散行列から主成分が求まるのかどうかを R で確認してみます。というのも、最初 prcomp 関数の戻り値の見方が分かりづらくて苦労したからです。

MNIST は次元が多すぎて見づらいので、R のサンプルデータである iris を使うことします。このデータは、アヤメの 3 品種 (setosa, versicolor, virginica]) について、がく片 (Sepal) と花びら (Petal) の幅と長さをそれぞれ計測したものです。つまりデータの次元は 4 で、サンプル数は 150 です。

> str(iris) 
'data.frame':   150 obs. of  5 variables: 
$ Sepal.Length: num  5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ... 
$ Sepal.Width : num  3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ... 
$ Petal.Length: num  1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ... 
$ Petal.Width : num  0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ... 
$ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ... 
> iris[1:4,] 
  Sepal.Length Sepal.Width Petal.Length Petal.Width Species 
1          5.1         3.5          1.4         0.2  setosa 
2          4.9         3.0          1.4         0.2  setosa 
3          4.7         3.2          1.3         0.2  setosa 
4          4.6         3.1          1.5         0.2  setosa 

prcomp 関数を実行します。また、PCA の結果は biplot で、主成分と主成分得点を同じ図にプロットすることが多いみたいなので、そのまま実行します。

> pca <- prcomp(iris[,1:4], scale=T) 
> biplot(pca) 

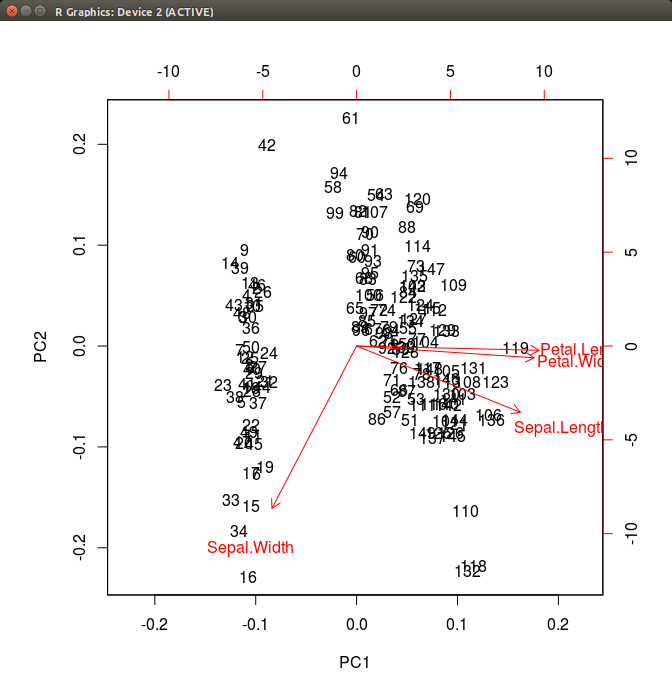
これだけだとよく分かりませんが、実は品種ごとにデータが綺麗に分かれています。こちらのサイトで同じプロットを色分けしたものが掲載されています。

主成分分析が簡単にできるサイトを作った - ほくそ笑む
http://d.hatena.ne.jp/hoxo_m/20120106/p1

ここで紹介したいのは、prcomp が返した pca というのは何か、という点です。str 関数で見てみます。

> str(pca) 
List of 5 
$ sdev    : num [1:4] 1.708 0.956 0.383 0.144 
$ rotation: num [1:4, 1:4] 0.521 -0.269 0.58 0.565 -0.377 ... 
  ..- attr(*, "dimnames")=List of 2 
  .. ..$ : chr [1:4] "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width" 
  .. ..$ : chr [1:4] "PC1" "PC2" "PC3" "PC4" 
$ center  : Named num [1:4] 5.84 3.06 3.76 1.2 
  ..- attr(*, "names")= chr [1:4] "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width" 
$ scale   : Named num [1:4] 0.828 0.436 1.765 0.762 
  ..- attr(*, "names")= chr [1:4] "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width" 
$ x       : num [1:150, 1:4] -2.26 -2.07 -2.36 -2.29 -2.38 ... 
  ..- attr(*, "dimnames")=List of 2 
  .. ..$ : NULL 
  .. ..$ : chr [1:4] "PC1" "PC2" "PC3" "PC4" 
- attr(*, "class")= chr "prcomp"

どうやら、5 つの要素を持つリストになっているようです。center, scale は iris データを標準化したときの値、rotation が主成分の行列、sdev が成分ごとの標準偏差、x が主成分得点になっています。pca には累積寄与率が含まれていませんが、summary 関数を実行することで、pca の sdev 要素を元に累積寄与率が計算されます。2 つの主成分で寄与率が 96% 近くあることが分かります。

> summary(pca) 
Importance of components: 
                          PC1    PC2     PC3     PC4 
Standard deviation     1.7084 0.9560 0.38309 0.14393 
Proportion of Variance 0.7296 0.2285 0.03669 0.00518 
Cumulative Proportion  0.7296 0.9581 0.99482 1.00000

試しに summary を使わずに寄与率を求めるとすれば、こうでしょうか。iris は標準化しておいたので、各次元の分散は 1 であり、4 で割れば全体を 1 としたときの累積寄与率が導出されます。

> pca$sdev * pca$sdev / 4 
[1] 0.729624454 0.228507618 0.036689219 0.005178709

pca で重要なのは主成分です。主成分は N 次元データを一次変換する行列なので、必ず NxN の正方行列になります。

> pca$rotation 
                    PC1         PC2        PC3        PC4 
Sepal.Length  0.5210659 -0.37741762  0.7195664  0.2612863 
Sepal.Width  -0.2693474 -0.92329566 -0.2443818 -0.1235096 
Petal.Length  0.5804131 -0.02449161 -0.1421264 -0.8014492 
Petal.Width   0.5648565 -0.06694199 -0.6342727  0.5235971

この主成分が、分散共分散行列の固有ベクトルなのでした。ということで実際に計算します。

> sdata <- scale(iris[,1:4]) 
> S <- cov(sdata) 
> pca2 <- eigen(S) 
> pca2 
$values 
[1] 2.91849782 0.91403047 0.14675688 0.02071484

$vectors 
           [,1]        [,2]       [,3]       [,4] 
[1,]  0.5210659 -0.37741762  0.7195664  0.2612863 
[2,] -0.2693474 -0.92329566 -0.2443818 -0.1235096 
[3,]  0.5804131 -0.02449161 -0.1421264 -0.8014492 
[4,]  0.5648565 -0.06694199 -0.6342727  0.5235971

> sqrt(pca2$values) 
[1] 1.7083611 0.9560494 0.3830886 0.1439265 

pca$rotation と同じ行列が得られました。また、固有値の平方根を取ったものが pca$sdev と等しくなっています。つまり分散共分散行列の固有値が主成分の分散になっていることも確かめられました。最後に、主成分を使って主成分得点を求めてみます。150 サンプル全部を計算してもしょうがないので、最初の 5 サンプルを取って・・・

> scale(iris[,1:4])[1:5,] %*% pca2$v 
pca2$values   pca2$vectors 
> scale(iris[,1:4])[1:5,] %*% pca2$vectors 
          [,1]       [,2]        [,3]        [,4] 
[1,] -2.257141 -0.4784238  0.12727962  0.02408751 
[2,] -2.074013  0.6718827  0.23382552  0.10266284 
[3,] -2.356335  0.3407664 -0.04405390  0.02828231 
[4,] -2.291707  0.5953999 -0.09098530 -0.06573534 
[5,] -2.381863 -0.6446757 -0.01568565 -0.03580287 
> pca$x[1:5,] 
           PC1        PC2         PC3         PC4 
[1,] -2.257141 -0.4784238  0.12727962  0.02408751 
[2,] -2.074013  0.6718827  0.23382552  0.10266284 
[3,] -2.356335  0.3407664 -0.04405390  0.02828231 
[4,] -2.291707  0.5953999 -0.09098530 -0.06573534 
[5,] -2.381863 -0.6446757 -0.01568565 -0.03580287

行列積の結果、pca$x と等しい値が得られることが確認できました。

ちなみに、PCA について書かれた英語版の wikipedia がやたら専門的で詳しいのですが、そのページの Derivation of PCA using the covariance method > Iterative computation セクションのところで、実際の高次元データで分散共分散行列を使って主成分を求めるのは効率が悪い、と書かれています。うまくアルゴリズムを書くと、共分散行列を全部計算しなくても主成分が求まるとかなんとか。

Principal component analysis - Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Principal_component_analysis